Introduction

After seeing ChatGPT’s surprising capabilities, it is natural to wonder how ChatGPT (and GPT systems in general) really work. The many explanations of GPTs on the internet are usually either written for the general public and consequently do not explore the fine details of the system’s operation, or else they assume that the reader is already familiar with AI. At the moment it seems difficult to find in-depth explanations of GPTs or AI in general which programmers and engineers will find satisfying. This article attempts to help fill this gap by giving a complete technical explanation of the structure of GPT systems without assuming any prior knowledge beyond what is common to anyone with a technical background. I will preface my explanation of GPTs with an overview of the nature of modern AI and the inherent difficulty of fully explaining any modern AI system.

Overview of Modern AI

Almost every major AI system today (GPTs, image and speech recognition, image generation, etc.) primarily consists of a neural network. What is a neural network? The Wikipedia Article on the topic gives a detailed explanation for those interested, but for the purposes of this article it is perhaps better to give an inductive sketch of the nature of neural networks rather than a formal definition.

Artificial Neural Networks

To begin with, neural networks are very different from computer programs. Although both run on computers, and take inputs and give outputs, neural networks, unlike programs, do not consist of a structured set of rules and operations. There are also no real datastructures in neural networks. Instead, everything in the input is translated into a collection of floating point numbers, this collection is then manipulated, and finally the resulting floating point numbers are converted into the output format (words, images, sounds, etc.) Further, the most important neural networks in use today (GPTs and image recognition and generation networks) have nothing analogous to loops or conditional branches. The operations done on the floating point numbers are identical for every possible input into the network. Thus, neural networks can be modeled as a giant mathematical function which takes in a list/vector of real numbers and outputs another list/vector of real numbers.

This giant function is not exactly designed or programmed by humans. Humans do create the basic function structure (or “architecture”), but the actual behavior of the function is defined by tunable constants inserted throughout the function expression. It is important to note that these constants do not change between executions of the function. For example, if you download an image recognition library, the function/network inside the library will have exactly the same constants every time you use it. These tunable constants in a function/network are only modified during the “training” process of the network. During the training process, the constants (generally called “parameters”) are modified so that the network gives the desired outputs for given inputs. In state-of-the-art networks, the number of parameters/constants can be extremely large. For instance, the network underlying ChatGPT has somewhere around 20 billion parameters.

Here are two analogies that might help clarify the distinction between architecture and parameters:

Analogy to Algebra

If we have a function , then

• The Architecture is the arrangement of multiplications and additions.
• The Parameters are the constant terms , , and .
• The Runtime Values are the input , the values of the sub-expressions, and the output value of the function.

Analogy to Tax Forms

On a multi-step tax form, we could say that

• The Architecture is the steps in the calculation (subtract line 10 from line 9, etc.)
• The Parameters are the constant amounts included on the form (e.g., a deductible of $12,550).
• The Runtime Values are the amounts you write on the form.

Summary

To summarize how this three-way distinction appears in neural networks:

• The Architecture only changes when the AI designers set up an entirely new network.
• The Parameters only change during the training process.
• When actually using the network (e.g., asking a chatbot questions) only the Runtime Values change. The architecture and parameters do not. This is similar to a basic algebra function or a tax form, where the expression shape and the constant terms are the same for any input value.

The tax rates and brackets are much more important practically than the structure of a tax form. Similarly, the actual operation of a neural network is primarily defined by the parameters, not the architecture. The architecture is more like a skeleton to hold the parameters, which are set by the automated training process.

Goals of Training, Validation, and Generalization

There are two main kinds of training (or “learning”): “supervised” learning and “unsupervised” learning. In supervised learning, there is a human-created collection of example pairs of inputs and desired outputs. A training algorithm attempts to find values for the parameters such that, for each input in collection of examples, the network gives outputs close to the desired output specified for the example input. Unsupervised learning does not involve a set of example inputs and outputs. Since GPTs are created with supervised learning, I will not go into detail here about how the network parameters are set in unsupervised learning.

Returning to supervised learning: in order to measure how well the network parameters have been configured, the example inputs are passed into the network and then compared to the desired outputs. A pre-selected function (called the “cost function” or the “loss function”) takes the results of the comparisons and combines them to produce a single number called the “loss” or the “error” for that specific configuration of constants/parameters. There are various different cost or loss functions that can be used, but they are usually similar the mean squared error function used in linear regression. (Because of this similarity to regression curve-fitting methods, a neural network is often called a “model”, because it attempts to model the relationship between the inputs and outputs in the set of examples. In fact, “model” and “network” are used almost interchangeably in AI. For the rest of this article, these terms will be treated as synonymous.)

The goal of the training process is to find values for the network parameters such that the output of the cost/loss function is minimized. In other words, to find values for the constants/parameters such that the outputs of the model are similar to the desired outputs specified in the set of examples. In using this process, AI researchers hope that if the configuration of parameters gives the desired results for the set of examples (that is, if the loss is low), then that configuration will also give desired results for new inputs not found in the set of examples. This is called “generalization.”

To give a more concrete example: if AI researchers are trying to create a neural network which automatically recognizes pictures of cats, they will create an example set of “cat” and “not cat” pictures. They will then use an algorithm to configure the network parameters such that the network can accurately give a result of “cat” or “not cat” for each image in the set of examples. Their hope is that if the parameter configuration gives accurate results for the example images, it will also give accurate results when presented with images not in the example set. If it does, then the network has “generalized”.

In order to confirm whether a parameter configuration constitutes a generalized network, the example set is divided into two subsets: the “training” set and the “validation” set. Usually the training set is much larger than the validation set. (e.g., the training set might consist of 90% of the examples, while the validation set consists of the other 10%.) The training algorithm only tries to minimize the loss for the examples from the training set. That is, as far as the “learning” is concerned, the network only “sees” the examples from the training set. To check how well the network is generalizing, the examples in the validation set are fed into the network, and then compared to the desired outputs in the validation set.

Does it really “learn”?

One might ask at this point how the validation set can be useful after it has been used once. Wouldn’t you need a new validation set every time you “test” the network with the validation set? Suppose you’re teaching a child arithmetic. If you give them a test, afterwards tell them they’ll be given an opportunity to retake the test, and then repeat all of the instruction you gave them before the test, and finally give them the same test again, will the test when given a second time be as good of a metric of their progress as it was the first time? Probably not, because after seeing what was on the test, they could have paid more attention to the material that was helpful for the particular questions on the test, without trying to really learn the material. Why isn’t this true when “teaching” neural networks? The training set is like the class instruction, and the validation set is like the test. The same training set and validation set is used throughout the whole process of configuring the network parameters. Why doesn’t the network just focus on learning the validation set?

The answer to this question is actually quite simple: the network has no reasoning powers or memory, not even the kind of memory that allows animals to be trained. The network is, in the end, just a large mathematical function with configurable constants. It cannot remember the test examples in the validation set in order to focus on those questions when it is shown the training set again. The network itself is not really “shown” anything and does not really “learn” anything. All that happens during “training” is the parameters/constants are reconfigured to minimize the loss.

Still, it’s easy to think of the network as “learning” or becoming “intelligent”. This is why the whole field is called “AI” (artificial intelligence) or “ML” (machine learning). The terminology is somewhat helpful, since there are certain isomorphisms between real human learning and the mathematical optimization done in machine learning. And of course, some argue that “real human learning” and “mathematical optimization” are not fundamentally distinct, because the scientific consensus is that the human brain is the result of evolution, which is a kind optimization for environmental conditions. Whether or not this is a coherent theory of human cognition is a philosophical question, and beyond the scope of this article. My point here is not to resolve the broad question of whether AI can ever become truly intelligent, or even to resolve whether it is in some sense “intelligent” even now. All I’m arguing is that we should be careful when applying the terms “learning”, “intelligence”, “knowledge”, etc. to neural networks as they currently exist. It’s easy when using these terms and seeing the impressive results of modern AI systems to imagine that state-of-the-art neural networks are quite similar to the human mind. As we’ll see in more detail below, this is definitely not the case.

Training with Gradient Descent

But we’re getting a bit of ahead of ourselves. Descending back to the purely technical level, the algorithm generally used to minimize the loss is the gradient descent algorithm, which works basically as follows:

1. Initialize all the parameters to random values.
2. Calculate, for each parameter, the derivative of the parameter with respect to the error.
3. Put all these derivatives in an n-dimensional vector, where is the number of parameters.
4. Normalize this vector, scale it by a factor called the “learning rate”, and then add the rescaled gradients to each of their respective parameters.
5. Repeat steps 2-4 until the error is reduced to a target value or cannot be reduced further.

This algorithm treats the error as a function of all the parameters. Since making a small change to any parameter will make a small change to the output error, this function is continuous and differentiable. Thus, we can take the derivative (technically the gradient, ) of this function and “walk downhill” until we find a local minimum in the function. This local minimum will be a configuration of network parameters such that there is a minimized difference between actual network outputs and the expected outputs from the training set. (That is, the error is small.)

There are various optimizations and modifications made to this algorithm in practice. For instance, the learning rate/step size is usually varied throughout the training. There is also a method called “backpropagation” which is used to efficiently calculate the gradient. But this article does not intend to explain the details of actually implementing a neural network, so we will pass over these practical points.

Summary so far & Realistic Hopes for AI?

To briefly summarize the explanation of modern AI given so far:

• Almost all AI systems today rely on artificial neural networks.
• Almost all artificial neural networks today are large mathematical functions taking numeric inputs and producing numeric outputs.
• The structure of the function is designed by humans, but the actual behavior of the function is defined by tunable constants called parameters.
• The parameters are generally tuned using a collection of example inputs and desired outputs.
• The hope is that by finding parameters that work for the examples, the network/function will give the desired outputs for inputs not found in the set of examples. That is, the network will be a general-purpose system for performing some task.

And now we come to what is probably the most important question regarding AI today: is this hope justified? The impressive performance of AI in answering questions, generating images, and recognizing images would all seem to indicate that this hope has been validated. It seems that the AI training algorithms have taken a small (at least proportionally small) set of examples and produced neural networks which can solve the general problem of image recognition or image generation or text generation, just as, for instance, a child comes to understand how to solve any multiplication problem even though he has been given only a small set of examples.

It is important to note here that it is not impossible that a mathematical algorithm without reasoning or memory could produce a function which implements the general solution to a whole class of problems. A multiplication computer program doesn’t really understand multiplication; it doesn’t, properly speaking, understand anything at all, since it doesn’t have a mind or even anything resembling a mind. It was, indeed, designed by humans, who do really understand multiplication, but it is not absolutely essential that a general-purpose algorithm be created by humans in order to be truly general-purpose. It is theoretically possible, for instance, that a program which randomly generated code trying to match examples of multiplication might eventually stumble upon the general-purpose multiplication algorithm.

Realistic Evaluation of capability

How can we determine whether someone or something really understands how to solve a problem in general? If we’re teaching a child multiplication, we can ask him to explain how he would solve a multiplication problem in general, not just how he solves some particular problem. If we’re trying to understand a randomly generated computer program that seems to implement multiplication, it will probably be more difficult to determine whether it does or does not implement a general purpose multiplication algorithm. This is because there are only a few ways of implementing a straightforward and efficient multiplication algorithm, but a huge number of ways of implementing a correct multiplication algorithm with convoluted code structure, pointless operations, and inefficient methods. Thus, if some algorithm randomly stumbles upon a general purpose multiplication algorithm, it is much more likely to stumble upon one of the convoluted and inefficient algorithms. Still, it will probably be possible to determine that it really does implement a general algorithm, because humans can “reverse-engineer” the code by restructuring it and deleting the pieces that do nothing, and then see what it’s actually doing.

It is much more difficult to do something similar with a neural network. As we saw above, the overall structure of the network is specified by humans, but this architecture is only a kind of scaffolding or skeleton. The actual operation of the network is defined by the millions or billions of floating-point constant parameters. The network cannot explain its behavior like a child can, and it is not clear how to restructure and simplify it in the way one could restructure and simplify a randomly generated program while keeping its operation identical. Without a method for explaining the operation of a neural network, it remains a giant black box of numbers which we can only hope will work in general.

Trying to make sense of how it works: “Neurons”

Currently, the only way of attempting to understand (or “interpret”) the operation of large networks is to look at individual “neurons” or groups of neurons and try to infer how they relate to other neurons and affect the network outputs. (In AI/ML, the word “neuron” has a technical definition, but for our purposes here we may think of it as a sub-expression within the giant mathematical function which defines the network.)

One note before proceeding: many discussions of reverse-engineering neural networks use wording that may lead one to believe that some particular neuron serves a purpose in the network. But it is arguably misleading to use “purpose” in this context because the values of the parameters/constants which determine the output of the sub-expression (i.e., the neuron) are only set by the mindless training algorithm to values that minimize the loss function. The sub-expression parameters only have “purpose” insofar as they contribute to the lower values of the error of the network as a whole. There is also no absolute guarantee that they have any “purpose” even in this sense, because they might have no significant effect on the loss function, just as much of the code in a randomly generated multiplication algorithm has no effect on the output.

At the moment, determining the “purpose” of individual neurons is not straightforward. Even OpenAI admits that at best they can look at what sort of inputs cause a particular sub-expression (i.e., a particular neuron) to evaluate to larger or smaller numbers, and then try to create some explanation of what “purpose” that neuron serves within the larger network. OpenAI experimented with using the larger and more advanced GPT-4 to create explanations of the neurons in the smaller GPT-2, but the explanations were largely unsatisfactory.

The situation is somewhat better when it comes to understanding image-recognition networks. The Circuits project provides a good overview of recent attempts at making the internal operations of image recognition networks understandable (usually called “interpretable”). The method used in the linked Circuits project article relies on a gradient ascent/descent algorithm: instead of tuning the parameters of the network to minimize the error of the whole network, they tune the inputs of the network to maximize the output value of an individual neuron or set of neurons. (A small change in the network inputs will only lead to a small change in the value of a particular neuron, so the function of neuron activation relative to input is a continuous and differentiable function, which allows gradient ascent.)

What do we find when using this gradient ascent method? One might expect, for instance, that we would find some neuron whose “purpose” was to recognize dogs, and so if we produced an image which maximized the output of that neuron, we would get an image which is a sort of Platonic form of a dog; an image which is as “doggy” as possible. This is not what happens. Instead, when we try maximizing various neurons that seem to be “for” recognizing particular things, we don’t get Platonic forms, but nightmarish images that, to human eyes, might bear only a superficial resemblance to what they are “intended” to recognize:

These and other experiments, such as the famous “toaster sticker” experiment, seem to completely disprove any theory which proposes that image recognition networks implement anything analogous to how humans recognize images.

There is no indication that the situation is any better as regards text generation neural networks such as ChatGPT. There are “glitch tokens” which cause ChatGPT to give bizarre responses when given certain prompts:

It seems clear that we can conclude from these many examples that both image recognition and text generation networks do not operate in any way at all analogous to human understanding of language or processing of visual stimuli. Neural networks (at least as they currently exist) seem to be incapable of actually learning anything analogous to what humans would call a universal. Current neural networks do not give results based on comparing particulars to abstractions; they give results by comparing particulars to statistical approximations of abstractions. By definition, this works very well statistically. But these statistical approximations only work up to a point. Before that point, it may seem that the network has really “grasped” something. But past that point, it generally becomes very clear that whatever the network is doing, it certainly isn’t doing something analogous to what the human mind is doing. Thus, it seems impossible to fully explain a neural network’s behavior in any other terms than “that’s what the math produces”.

However, it is possible to explain the structure of a neural network, the “scaffolding” which defines how the network parameters interact. As we have seen, this definitely does not explain how the network “really works,” but it does help us have at least some concept of how the network works at a very broad level. It will also allow us to recognize what tasks the network is fundamentally incapable of performing simply because the network structure does not allow it, regardless of parameter values. Because GPTs are currently the kind of network most likely to have a significant impact on society, I will in this next section try to give a detailed explanation of the overall structure of a GPT neural network.

GPT Structure

First of all, what is a “GPT”? You may have seen that it stands for “generative pre-trained transformer,” but if you’re unfamiliar with AI terminology, that probably isn’t very meaningful. “Generative” at least is relatively easy to understand: GPT neural networks generate text. This distinguishes them from other older pre-trained transformers which could not generate new text, but could only perform operations and make judgements about input text. The “transformer” part will be explained in detail below. But before we get to that, I’ll explain what “pre-trained” means.

Pre-training

As described above, during network training, the error can be seen as a function of all the parameters. The goal of the training process is to find a local minimum in this function which is hopefully the absolute minimum. But what if we want a new parameter configuration (of the same network) for a different but slightly related task? Do we need to retrain/reconfigure all the parameters from scratch? AI researchers have found that this is generally not necessary. Instead, one can begin with the old network parameters (trained to a local minimum in the old error function), and then use gradient descent to find a new local minimum in the new error function, which will likely be near the old local minimum. (We use “near” here because we can think of the parameter configuration as a coordinate in n-dimensional space, where n is the number of parameters.) This retraining process is much faster (and thus cheaper) than starting training completely from scratch, because there is much less “distance” to be covered in the n-dimensional parameter space. Because there are often many specific tasks that are closely related to some general task, usually a general network is trained first, and then that general network is retrained for the specific tasks. For example, answering medical questions and answering questions about a commercial software package are both tasks related to language processing. So a medical company might take a base network trained for a generic language task and then retrain it for its specific task (answering medical questions), and a large software corporation might take the same base network and retrain it for its specific task (answering user questions about its large software suite).

This relatively fast/cheap retraining for some specific task is called “fine-tuning” and the initial slow/expensive training for a base model is called “pre-training”. But why does fine-tuning work? Suppose we train from scratch a large network with an error function which measures how well the network predicts the most likely next word after a long string of previous words. We’ll end up with a model that performs well at this task (text prediction). But why would we expect fine-tuning to result in a model which works well at a different task (such as answering medical questions)?

The general explanation for the success of fine-tuning is that by “teaching” the network to perform a generic language task (text prediction), the network will “learn” general facts about language (nouns, adjectives, sentence structure, etc.) and then be able to reapply this general “knowledge” to a specific task. But as explained above, the use of terms like “learn” and “knowledge” are somewhat misleading when applied to neural networks, because the network only is a statistical approximation of human behavior. If we want to describe the fine-tuning process in more precise terms, we might say something like this: during training, subexpressions of the giant network function can come to have values which are correlated to certain aspects of the input data. For instance, when the parameters are randomly initialized, there might be some subexpression in the network which is, by accident, very slightly correlated with whether or not the last word in the input is an adjective. Fiddling the parameters in this subexpression might increase this correlation and also decrease the error, and so by the end of the training process the value of the subexpression may be very well correlated with whether or not the last word in the input is an adjective. Thus, by the mindless gradient descent process, subexpressions in the network can come to have correlation with some meaningful aspect of the input. And again, this correlation is statistical and accidental: there is no necessity that any particular subexpression in the human-defined network structure ends up correlated with any particular aspect of the input. If the same network structure is retrained from scratch, starting with different randomly chosen starting parameter values, the same subexpression in the new parameter configuration will likely be correlated to some completely different aspect of the input data.

This is the mechanism underlying the success of fine-tuning. The smaller subexpressions in a large network trained for a particular task are likely to end up correlated with some more basic aspect of the task. The larger subexpressions will generally combine the values of the smaller subexpressions and end up correlated with some more complicated aspect of the task, and the full expression defining the network output will be correlated with the whole task itself. During the retraining which takes place during fine-tuning, generally only the parameters defining the more complicated subexpressions will require modifications, while the smaller subexpression parameters can be “reused”. If, for example, some expression in the generic text-prediction network configuration was already correlated with “is the last word an adjective”, the gradient descent for the new question-answering network can “reuse” that correlation when configuring the larger expressions to be correlated with desired results for the question-answering task, since both text-prediction and question-answering will probably require some subexpression to be correlated to something about adjectives.

Coming back to ChatGPT: the network underlying ChatGPT is actually a fine-tuned network. The base parameter configuration was only trained for next-token prediction (given a sequence of words, it could predict the most likely next words). By fine-tuning this pre-trained generic next-token prediction model for the specific task of interacting with a user in a conversational format, OpenAI produced the parameter configuration which is used by ChatGPT.

Transformers

And now we can finally come to a discussion of the structure of a GPT; the human-designed giant mathematical expression which contains the parameter values as tunable constants. Technically, the term “GPT” does not refer to a particular network structure (that is, to a single standard mathematical expression underlying every GPT network). Rather, it refers to a whole class of network structures which have similar “shapes”.

Below is a very minimal example of that common shape:

The red blocks represent subexpressions which contain many parameters, the black blocks represent subexpressions which contain no parameters, and the green blocks represent “runtime” values of the subexpression; that is, values of the subexpressions which exist when calculating the network results for a particular input value. Any box which has the same label is exactly identical wherever it appears in the network.

Let’s go over the overall structure and then “zoom in” and look at particular pieces in more detail.

The task of a GPT is relatively simple: take previous words in, and give a next word out. This is the case both for generic next-token prediction and for answering questions as in ChatGPT. But, of course, ChatGPT can output more than one word. How does this work if the basic network structure only supports outputting one word at a time? The process proceeds basically like this:

1. Take all previous messages (including ChatGPT’s previous messages along with the user’s messages) and use them as the input text for the network.
2. Predict the next word using the network
3. Add the predicted word to the output message. It will thus be included in the network input the next time around.
4. Repeat steps 1-3 until a special “end of message” symbol is predicted as the mostly likely next word.

Because previous messages are used as input for the network, ChatGPT can seem to “remember” the history of a conversation and base its responses on information not present in the immediately previous message.

However, this memory does have a limit: the network is generally only designed to work with a certain number of tokens. In ChatGPT this limit is 4096 tokens. (ChatGPT is actually not a word prediction network. It takes “tokens” as input and output, which for our purposes here you can think of as syllables, although it’s a bit more complicated than that in practice. ChatGPT splits the input text up into tokens, feeds it through the network, and then rejoins the output tokens into text.) In our example network, the token limit is only 3 tokens.

There are three main sections or stages of data manipulation in a GPT network:

1. Input Stage: This is where words/tokens are taken in by the network and then converted into numbers (or more specifically, lists of numbers called “vectors” or “tensors”). On the diagram, this is all the stuff to the left of the big black-bordered boxes.
2. Transformer Stack: This is all the black boxes in the middle of the diagram. This is the core of the network and where the '“interesting stuff” happens. It’s important to remember that the vectors inside the network don’t correspond to individual words. Asking what, exactly, they do correspond to is like asking what a neuron in an image recognition network corresponds to, which, as noted above, is in a sense impossible, because they may not correspond to anything at all, or they may correspond only to a statistical approximation of something meaningful. All we can say is that the vectors correspond to the results of the mathematical operations which produce them.
3. Output Stage: This is the stuff on the far right of the diagram. This is where the output vectors of the transformer stack are decoded into output words/tokens.

We’ll now explore each section in detail.

Note: in the explanation below, I have asterisked a few terms with [*]. These are terms which I found helpful in describing the internals of a transformer, but which are not terms used in other papers or posts about transformers. Standard terms are not asterisked.

The Input Stage

In the input area, each input token is converted into a one-hot vector with a length equal to the model vocabulary size, where the one-hot component is the index of the token in the vocabulary. (By “one-hot vector” we mean a vector where a single component/axis has a value of one, and all the other components/axes are zero.) This one-hot vector is transformed by a matrix multiply with the embedding matrix into an embedding vector which represents the word numerically. This vector is usually very long (several hundred elements or more). Word embeddings are a standard part of modern AI. The idea behind a word embedding vector is that words which are more related to each other will have embedding vectors which are closer to each other in “embedding space,” and axes in embedding space (i.e., specific indices in the embedding vector) will capture some aspect of a word. The conversion between words and embeddings is specified by trainable parameters. (i.e, the training process determines what embeddings to use for each token in the model’s vocabulary.) Because of how matrix multiplication works, multiplying the one-hot vector by the embedding matrix , is equivalent to taking a particular column out of the embeddings matrix, as if it were a table.

As shown in the diagram, the same embedding matrix is used for every token in the input. e.g, if the token “house” appears multiple times in the input, it will have exactly the same embedding vector each time.

The embedding vector is added (component-wise) to a positional encoding vector to produce the layer 1, token attention input vector[*] The positional encoding vector is not trained, but it is different for each input token number . Its purpose is to allow the attention heads in the upcoming transformer stack to have different behavior based on the token number. (This will be explained more below.) Usually, the positional encoding vector is constructed by setting each component in the vector to a value which is calculated by taking the taking the token index and passing it through a sine or cosine function whose frequency varies based on the vector component index. The graph below illustrates an example positional encoding table:

The Transformer Stack

General architecture of the transformer stack

The transformer stack consists of several sequential layers. The number of layers can be easily reconfigured without fundamentally changing the basic architecture of the network (input, transformer stack, output). In AI, values like this are called “hyperparameters”. They affect how the network is shaped (its “topology”) or how training proceeds, but they are not part of the training process itself. There are only 2 layers in this example network diagram, but there are usually many more layers in a state-of-the-art GPT. The GPT-3 network (a larger version of the GPT-3.5 network underlying ChatGPT) has 96 layers.

Each layer takes, for each token , the attention input vectors[*] (produced either by the input area, if , or by the previous layer otherwise), and produces a new vector which will be used as the input for the next layer. The output of the last layer is passed into the Output Stage[*] which will be discussed later.

The attention mechanism

There are three boxes shown in the diagram in each layer for each input token (e.g., in the first layer, there are boxes for “Layer 1, Token 1 Attention”, “Layer 1, Token 2 Attention”, and “Layer 1, Token 3 Attention”). But this is primarily to make the data flow clearer. In reality the operations performed for each token are almost identical. I’ll explain this in more detail below, but first I’ll explain what these repeated operations are.

The attention heads are the core of a transformer (in fact, the word “transformer” just means a network centered around attention heads). In our example network, there are actually only four attention heads:

• Layer 1 Attention Head 1
• Layer 1 Attention Head 2
• Layer 2 Attention Head 1
• Layer 2 Attention Head 2

All of these heads are applied once to each token. (Hence each of them appears three times in our diagram.) But what does “attention” mean and what is an “attention head”? At a very high level, the whole “attention”/“attention head”/“transformer” network structure was created to give the training algorithm an efficient way of defining subexpressions which approximately capture important aspects of structured input. Put another way: the attention-based network design helps the network to “think” about structured input such as sentences. As evidenced by the success of ChatGPT and other transformer-based AI models, the attention/transformer network structure does seem to be more successful at language tasks than older, non-transformer network structures. In order to get a sense of why this is the case, we will have to look at the mathematical structure of the attention system.

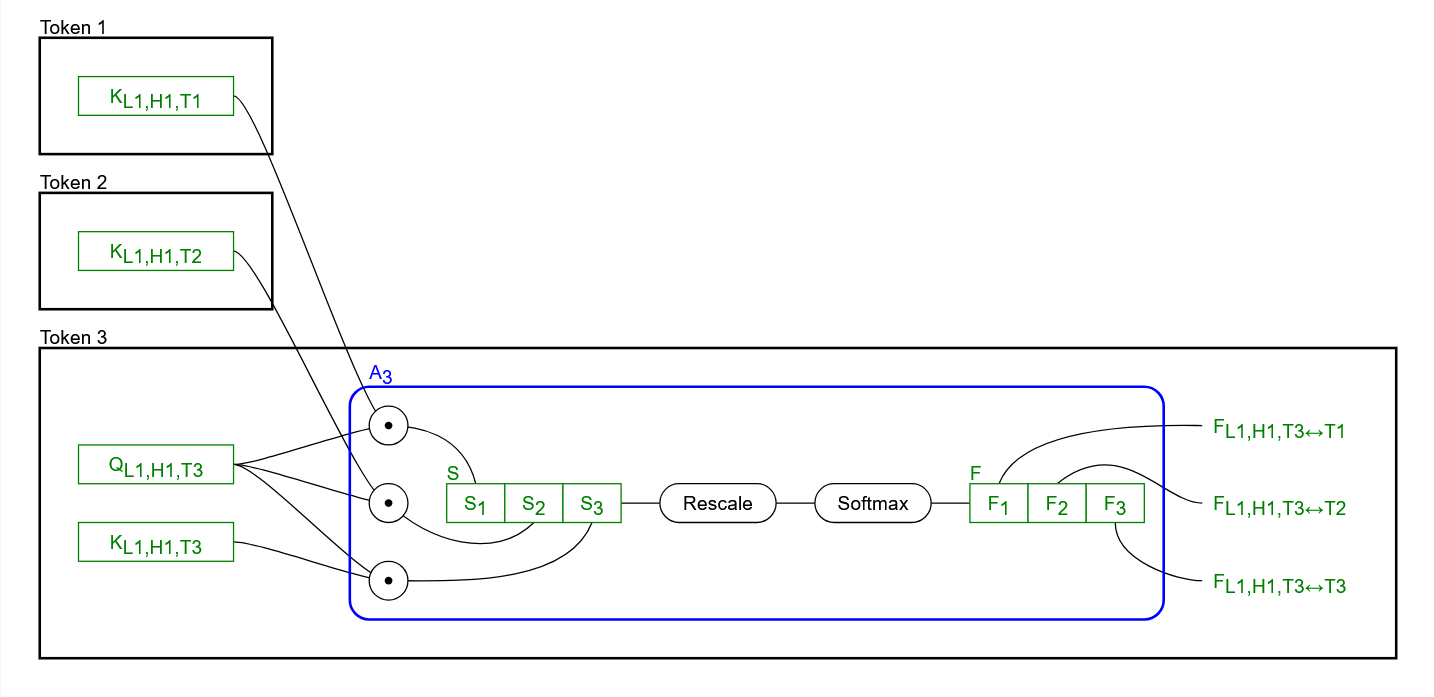
As noted above, there are actually only four attention heads in this network, each repeated three times, and if you look at the diagram, they all share a very similar structure. Before getting to how the attention heads interact and why this structure is duplicated so many times, I’ll explain the operation of a single attention head. For reasons that will become clear in a bit, I’ll focus on a token three attention head. Here it is:

On the left, we have the attention input vector[*] that was produced by the input stage. This vector is then passed through a layer normalization operation. AI researchers have found that interspersing layer normalization operations throughout a network seems to speed up training. I won’t attempt to explain here why layer normalization has this effect. I’ll just go through the layer normalization operation itself. At a high level, layer normalization is an operation that takes in a vector (in our case, ) and outputs another vector. The output vector is calculated as follows:

1. Calculate the mean and standard deviation of the input vector.
2. Normalize the vector by subtracting from each component and then dividing by . The new vector will have mean 0 and standard deviation 1.
3. Take the new vector and multiply it (component-wise) by the trainable gain vector . Then add another trainable vector, the bias vector .
4. Output the result.

To summarize, if is our input vector, and is our output vector, we calculate each component using the formula:

Or, in vector terms: , where denotes the component-wise multiplication operator. (Technically, this is the Hadamard product, but in computer programming barely anyone ever calls it that.)

After we’ve normalized the attention input vector[*] , we pass it through three trainable matrices: the query projection weight matrix , the key projection weight matrix , and the value projection weight matrix. As indicated by the diagram, these matrices are used by all of the instances of Layer 1 Attention Head 1. The “×” operation here denotes a simple vector-matrix product (i.e., a linear transform) which produces three new vectors: the query vector , the key vector , and the value vector . These vectors are usually significantly smaller than the attention input vector from which they are produced, but they may still be rather long vectors (a few dozen elements or more).

These vectors are then passed through the self-attention scoring operation[*], denoted here as . (The “3” is for token 3, because the attention scoring operation proceeds slightly differently for other token numbers, as will be described later). The scoring process is relatively straightforward, but to simplify the diagram, it was compressed into a single symbol. Here’s what it looks like if we expand it out:

The blue box is what is represented in the big diagram by the circle. In this box:

1. The query vector is multiplied (by a dot product) with the key vectors of every other token (including its own key vector, ). This produces the scores vector , which contains the results of all the dot products.
2. This vector is linearly rescaled, usually by dividing by the square root of the number of tokens. (i.e., in this case, each element of would be divided by )
3. The whole vector is passed through the softmax function.
4. The three components of the vector are split out into the three scalar values , , and , which you see in the big diagram.

These three scalar values are then used to linearly rescale the vector of their corresponding token. e.g., . These three vectors are then added (component-wise) to produce the attention head output vector[*] .

What is the point of this whole operation? Why does using transformers seem to produce neural networks which are much more successful at language tasks? The standard explanation is that the attention mechanism allows tokens to easily “talk” to one another: through the key vector, a token can “advertise” what information it has, and then other tokens can “ask” for it through the query vector, and finally the tokens can “share” information through the value vectors.

What if a token wants to “ask” for information from a token some number of tokens before it? This is where the positional encoding comes in: the different frequencies of the positional encoding vector allow the attention mechanism to “know” where it is relative to other tokens, and include that in its queries and keys.

Multiple heads and multiple tokens

So we’ve looked at one attention head for one token. What about the other attention heads and the other tokens? If you look at the diagram, you’ll see that for token 3, the structures of Layer 1 Attention Head 1, Layer 1 Attention Head 2, Layer 2 Attention Head 1, and Layer 2 Attention Head 2 are all exactly identical. The only difference between the different attention heads for token 3 is that different query, key, and value projection weight matrices are used.

What is the difference between the different instances of the same attention head across tokens? That is, what is the difference between the three instances of Layer 1 Attention Head 1 in tokens 1, 2, and 3? You’ll see in the diagram that the only difference is in the result of attention scoring operation . Let’s look at this more closely:

• In token 3, the attention scoring operation produced three scaling factors, relating token 1 to token 3, token 2 to token 3, and token 3 to token 3.
• In token 2, the attention scoring operation produces two scaling factors, relating token 1 to token 2, and token 2 to token 2.
• In token 1, the attention scoring operation produces only one scaling factor, relating token 1 to token 1.

If you look at the links, you’ll see that the operation only “looks at” (takes data from) its own token, and previous tokens. So token 2 doesn’t look at token 3, and token 1 only looks at itself, and not token 2 or token 3. The attention scoring operation “ignores” tokens after its own. (Actually, the operation does bring them in, but through a mathematical trick, they get multiplied by 0 and so they drop out.) Before I explain why this is part of the network design, I’ll go over how this works at a technical level.

Implementation of masked self-attention

Note: if this section is too technical for you, feel free to jump down to “The purpose of masked self-attention”

Above, I explained that the attention scoring operation operates basically like this:

1. Take the dot product of this token’s vector with every token’s vector. Put all those dot product results in a list/vector.
2. Rescale the list.
3. Run softmax on the whole list.
4. Split out the components into the factors used to scale the vectors from each token.

This is correct for token three (the last token), but if we want to generalize the algorithm for all tokens, there’s another step we need to add:

1. Take the dot product of this token’s vector with every token’s vector. Put all those dot product results in a list/vector.
2. Rescale the list.
3. Set to every component after this token.
4. Run softmax on the whole list.
5. Split out the components into the factors used to scale the vectors from each token.

For token 3, this new step does nothing: token 3 is the last token, so there aren’t any tokens after it. But what does it do for the other tokens which aren’t last? Won’t adding break stuff?

The part is actually a trick for setting those components to zero in the final result. If we look at the softmax formula we’ll see why. In order to calculate the component of the softmax output vector for an input vector , we use the formula:

Now watch what happens if we set the component of to . That is, if we set , we get

So that component in the output vector is set to zero. Notice what happens in the other components of : since will drop out of the sum in the denominator, it will be as if those other components were calculated by softmax on a smaller vector with deleted entirely!

If we were to insert all this into our diagram of the attention mechanism, we’d get something like this:

The output list is still n elements long, it’s just that some of them have been set to zero. Let’s see what happens in the big diagram if we break out into three scaling factors, just as we did in token 3. If we do that for token 2, we’ll get this:

But because of the stuff described above with softmax, that last factor will be zero:

And, consequently, so will the vector it produces:

Since adding zero does nothing, we can delete that factor and that vector, and we end up with the operation shown in the diagram to begin with:

(In the end, then, the attention mechanism is basically identical for every attention head. The only difference is at what index the replacement is applied.)

As noted above, since the softmax was calculated as if the component for token 3 wasn’t there, the remaining factors will be identical to what they would be if token 3 didn’t exist at all. In other words, because of the “set to ” step, we have made token 2 be calculated as if it were the last token in a model with only two tokens. This is called “masked self-attention” because of the insertion which “masks” future tokens and causes each token to ignore information from those future tokens. (There are transformers which use non-masked attention, without the trick. But ChatGPT and other major GPT-based systems today use masked attention.)

The purpose of masked self-attention

Why is this useful? Imagine we had a network which took as input not three tokens but several thousand tokens (as does ChatGPT and other real-world GPT systems). Suppose we gave the network a question 50 tokens in length, followed by a special “end of question” token (thus filling up the first 51 tokens), and wanted to use the network to get the most likely answer. We could set all the other tokens after the 51^st token to a special “empty” token, but it turns out that those tokens don’t matter at all. All we care about is the final output output token at that 51^st position, which will tell us the most likely starting token of the answer to the question. Because of the process described so far, we only have to look at tokens 1-51 in order to calculate the output of token 51. All the subsequent tokens and their transformer stacks don’t enter into the calculation of that token at all.

What do we do with that token? We add it to the answer we’re showing to the user, but we also put it in the 52^nd position of the network inputs, and the output for the 52^nd token will give us the most likely token for the second token of the answer (i.e, token 53), and so on. This repeated process of producing new tokens is called inference.

Now, when we add a new token to the gradually increasing collection of network inputs, do we need to recalculate all of the previous tokens? We actually don’t need to, because the calculation of the transformer stack for each of those tokens only looked at previous tokens. So in order to add a new token, all we have to calculate is the transformer stack for that new token, using the already calculated values for previous tokens. This massively decreases the number of calculations we have to do when building up a response using the network.

Because of this, it actually turns out that there isn’t a hard limit on the maximum number of input or output tokens. The positional encoding is calculated from sine and cosine functions, so we can just keep extending the positional encoding indefinitely, and keep tacking on more tokens. In practice, however, this doesn’t work very well because the model was trained only on sequences up to a certain length. So it doesn’t “know what to do” with sequences longer than that length, and GPTs generally start spewing nonsense if you try to generate output longer than the maximum input sequence length the network was trained with. There are various methods of working around this problem (e.g., “ALiBi”), but I won’t go into them here.

Merging attention heads

What do we do once we have the output of the attention heads? We need to have a single output vector for each token, but so far we have one vector from each of our two heads. So, for instance, in token 3, we have from head 1, and . How do we get to the token 3 layer 1 output vector ?

First, we concatenate (||) the vectors from the two attention heads, and then pass the concatenated vector (by a simple matrix multiply/linear projection) through a trainable matrix . As you can see in the diagram, this same matrix is used for all the tokens in layer 1. This projection operation produces a merged vector .

We then do something interesting: we add this vector to the original input vector that we had before doing any of the layer normalization or attention stuff. This is called a “residual connection” or “skip connection”. Why do we do this? Like layer normalization, residual connections are another technique that AI researchers have found increases training speed. And again, I’m not going to get into the probable reasons why it works.

After adding our original vector, we pass it through another layer normalization operation. This is identical to the previous layer normalization, except with different trained gain and bias vectors: and . These are used by every token in the layer.

After this layer normalization, we pass the vector through a feed-forward network (also called a “multilayer perceptron”) with one hidden layer. A feed-forward network is actually a very commonplace operation in modern AI, and a lot of explanations of GPTs don’t go over this step in detail because they assume that readers are already familiar with the term “feed-forward neural network with one hidden layer”. But since I’m writing for people who don’t have any prior AI experience at all, I’ll give a detailed explanation here. (And again, this isn’t specific to GPTs.)

Aside: The Multilayer Perceptron

The multilayer perceptron is the oldest (or close to the oldest) kind of neural network. However, since the focus of this article is to explain how neural networks work, I’ll leave an exploration of its history as an exercise for the reader. Let’s first take a look at its overall structure. If you look online for a diagram of a multilayer perceptron, you’ll find a lot of strange, weblike diagrams that look something like this:

This is a mostly accurate description of the basic structure, but it’s hiding a lot of complexity. Let’s take a look at a more detailed diagram:

As in our big diagram of a GPT, the red boxes are trained values, the green boxes are runtime values, and the black circles are static operations. This whole diagram is what is depicted in the big diagram by the little “FF” circle. This is what we would see if we could take a microscope and “zoom in” on that circle.

As in the big GPT diagram, data flows from left to right and there are no loops. Here are the main stages of the computation process:

• On the far left, we take in the input to the feed forward network, which, if we zoom back out, we’ll see is the vector . Here, it’s just labeled , and it’s split up into its scalar components. (It’s important to note, however, that in a real GPT network, will have far more than three components. is shown here with only three components to simplify the diagram.)
• We then have the hidden layer. Each box is one of the circles you see on a standard diagram of a feed-forward network with one hidden layer.
• As you can see, the structure of each box/neuron in the hidden layer is identical. The only difference between them is that each neuron/box has its own parameters.
• After the hidden layer, the results of each neuron of the hidden layer are collected into a vector .
• Then we have another layer of neurons with a similar structure to the neurons in the hidden layer. If you look carefully, you’ll see that in the output layer, there isn’t the little operation. The denotes the activation function, which we’ll get to in a bit. In the feed-forward network used in a GPT, there is no activation function on the output layer, but this is not necessarily the case in other feed-forward networks found in other AI contexts.
• One final point about the diagram: unlike in our GPT diagram where a single green or red box could represent an entire vector or matrix, in this diagram every box represents a single scalar value. So, for instance, the box represents a single trainable parameter.

Now let’s take a look at how a neuron works. Since all of the neurons in the hidden layer are identical except for their parameters, we’ll just focus on Hidden Layer Neuron 1. The stages of calculation in a neuron are fairly simple:

1. The input vector is copied to that neuron, and then multiplied (by a dot product) with the weights vector . The weights vector in this diagram is equivalent to what other explanations of feed-forward networks might call the the link weights.
2. A dot product produces a scalar value, to which we add the basis parameter
3. The result of this addition is passed through the activation function . In the early days of artificial neural network research, the activation function function was meant to simulate how real biological neurons fire. There are various activation functions that are used in ML. Some standard ones are the hyperbolic tangent function or the logistic function, but the most common activation function used today is the “rectified linear unit” (usually abbreviated “ReLU”). It sounds complicated, but it’s just .
4. The output of neuron 1 is just the output of the activation function.

The calculation of the output layer neurons is identical, except we skip the activation function and just output the result of the addition. (Or, if you want to think of it with an activation function, we just use .)

We then collect the results of all the neurons into a vector, and that gives us the network output , which in the big diagram, is .

So that finishes the feed-forward neural network shown as “FF” on the big diagram. The box at the top of the diagram represents all of the weight and basis parameters in the feed-forward network, which are shared by all of the tokens in layer 1.

To finish the calculation of one token, we add this feed-forward network output to another residual connection going back to the value before the network, and then that becomes the output vector for the first layer, which is also the input vector for the second layer.

Output Stage

Almost done! As we’ve noted above, when we run a GPT on a collection of tokens, the final output is the most probable next token. How do we take the results of the transformer stack and turn it back into a token? This is what the output stage[*] is for. Compared to the rest of a GPT, it’s relatively simple.

The final output of the transformer stack for the token (e.g., for token 3) is passed backwards through the embedding matrix. In the input area, we projected the one-hot token vector through the embeddings matrix to get a word embedding vector, which then got passed through all the other transformations in the network. At the end of the network, we end up with a vector of the same length as the word embedding vector. By multiplying it with the inverse () of the embeddings matrix, we get a new vector with a length equal to the token vocabulary size.

This new vector is called a “logits” vector. It has the same length as the one-hot token vector in the input, except each component of the logits vector will have a different value, unlike on the input side where a single component in the token vector was 1 and all the others were 0. The magnitude of the different components of the logits vector are related to how strongly the transformer “thinks” that the next token is the vocabulary word corresponding to that vector index. Why is this called the “logits” vector? Practically speaking, the term “logits” just refers to a raw network predictions vector before it is normalized. There is, of course, a historical reason why this came to be called a logits vector, but it’s not generally discussed in practice.

So the logits vector is the “raw” predictions of the most likely next word/token. There may be positive and negative values in the logits vector, and to get final token probability predictions, we pass the logits vector through the softmax operation (denoted here by ). Because of how softmax works, each component in the resulting token probabilities[*] vector will have a value between 0 and 1, and the whole vector will sum up to 1. Since the vector is the same length as the length of the model’s vocabulary, we can look at this vector as the network’s “prediction” of the probability that any particular token/word of the vocabulary is the next token. To get an single output token, we use some token picking operation to take this token probability distribution and select just one token. The list is sorted by probability, and then either the most probable token is selected, or, to add variety, some other token near the top of the list is chosen.

Conclusion

To sum up everything we’ve learned in this article:

• Neural networks are big statistical approximations (or “models”) of the training data.
• These statistical approximations usually give very strange results for some inputs, indicating that their operation is definitely not analogous to the operation of the human mind.
• Transformers consist of three stages: the input stage, the transformer stack, and the output stage.
• The input stage converts input words/tokens into a vector ready to be passed to the transformer stack.
• A transformer block is identical for each token, but it doesn’t look at future tokens. The attention mechanism allows the tokens to “talk” to each other, enabling the whole network to build up a structured understanding of the input.
• The transformer stack consists of many stacked transformer blocks.
• The output stage takes the output vectors from the transformer stack and converts them to words/tokens.
• The whole process only outputs one token at a time. Each output token is appended to the input and then the process is repeated in order to gradually build up a complete response.

How should this affect our thoughts about GPTs? Although it may initially seem counter-intuitive, I think the first conclusion we should draw from this is that GPTs are relatively simple. Yes, you just read several thousand words explaining how they work, but now that you have at least some grasp of the whole system, go back and look at the structure of the attention mechanism and the structure of a feed-forward network. The entirety of the complicated parts of the whole system is in those two diagrams. Everything else is either matrix multiplications or the fairly simple layer normalization operation. These diagrams are, indeed, somewhat complex. But these structures are much simpler than, say, a modern CPU or even a moderately large web app. A modern app has a huge variety of different data structures and submodules, while a GPT has just a few basic structures which are repeated thousands of times.

Still, the runtime operation of a GPT is defined mostly by the parameters, not by the network structure. And as described above, we don’t currently have a good way of really analyzing the runtime behaviors which emerge from these parameter configurations. We can, however, reach a better understanding of some of the strange behaviors of these networks by looking at their structure.

Take, for example, the major problem of hallucinations. At root, GPTs are just text predictors, and ChatGPT and similar AI chatbots are just text predictors which have been fine-tuned for the task of predicting answers to questions. Since these networks have been trained on giant piles of text scraped from the internet, they are specifically next-token predictors which try to predict the most likely next token if the input text were internet text.

If a human was asked to come up with some text that sounds like it could appear on the internet after the words "A paramagenetic hyperspace flux rectifier is a ", a human would probably assume that the text would likely appear in the context of some fictional sci-fi world, and would make something up that would fit with that. (e.g., “A paramagenetic hyperspace flux rectifier is a device used in a warp core to stabilize the fields around a ship and enable safe space travel.”) Because their goal was to create a plausible continuation for the text that was given to them, they probably would not say something like “A paramagenetic hyperspace flux rectifier is a made-up term which doesn’t appear in any major sci-fi universe that I know of, but maybe it’s a term in some other fictional universe,” since that isn’t what you would likely see on the internet after something which was obviously a stereotypically sci-fi term. However, if you ask a human for a factual response, they will tell you that it’s obviously fictional. The answers people give to questions depend heavily on context.

How does ChatGPT handle this problem? It’s fine-tuned to give accurate, factual responses, unless you instruct it otherwise. It seems to do this fairly well:

But if you just ask ChatGPT generically to “continue a sentence,” it generates a plausible internet-like continuation, without any cautionary note that it’s a fictional term:

(Although, if you ask it more questions, ChatGPT says it is a fictional idea and it was only giving a speculative/imaginative answer.)

So far so good. It seems ChatGPT has been fine-tuned well enough that it “knows” that it’s supposed to give factual answers and not just the most likely internet text. But then we try questions like this:

What happened? ChatGPT has seen so many discussions of the Monty Hall problem on the internet that whenever it sees something that really looks like the Monty Hall problem, it jumps to what is almost always the most likely answer when presented with something which looks like the Monty Hall problem.

Bing Chat, which uses GPT-4 (a more advanced version of the network powering ChatGPT) manages not to fall for the transparent door puzzle:

But it isn’t hard to make a prompt that does fool it:

How can these systems seemingly be so smart but still make obvious mistakes like this? One explanation you’ll often see is that ChatGPT is just a stochastic parrot or a “Blurry JPEG of the Web”, and consequently it has no real understanding of logical reasoning, but only repeats the information in its training data. Especially after learning about how GPTs actually work at a low level, this can seem like a fairly complete explanation: the loss function is calculated based on how accurate the network is at predicting next tokens, and the training process is designed to minimize that error. We would expect the model to give answers just based on statistics, without anything like logical reasoning. This mental model of GPTs is definitely more accurate than the standard marketing about the power of AI. But it’s still a bit too simple.

It’s true that the network is, in the end, just a big pile of transformer blocks and statistics. But it’s easy to forget just how big that pile is. The 20 billion parameters in ChatGPT and the estimated 1 trillion parameters in GPT-4 leave a lot of room for very complex behavior that can go beyond what most people will imagine when they hear the term “statistical model of the internet.” The post “The Stochastic Parrot Hypothesis is debatable for the last generation of LLMs” gives some persuasive arguments that this concept of GPTs fails to account for some of the behaviors of GPT-4. The post author gives this exchange as an example:

ChatGPT’s response to the question is on the left, GPT-4’s response is on the right. GPT-4’s response demonstrates an ability (or at least an apparent ability) to connect and reason about different facts in an imaginary spatial situation. Was GPT-4 given an example in its training data which was close enough to this situation that it can just parrot back a response? Maybe. But the more plausible explanation is that GPT-4 builds up something like an internal model of the world while reading these sorts of prompts, and then consults it to answer them. That seems to be something more advanced than just a “stochastic parrot”.

One could perhaps argue that even these complex responses are just a more advanced form of stochastic parroting, since GPT-4’s more advanced response is in the end more likely than ChatGPT’s more simplistic response. But what, then, does “stochastic parrot” really mean? If all we mean by “stochastic parrot” is that all the responses it makes are in some way derived from its training data, then it’s a stochastic parrot by definition. But if we think, instead, that GPTs are just a scaled-up dissociated press algorithm and can only repeat (with some modifications) what already exists in the training data, then these experiments seem to show that we need a better model of what GPTs are really doing.

I can’t give many answers in this article, or even give all the questions. I’ve only scratched the surface of what AI is and what we should expect from it. If you started reading this post looking for answers, I hope you found some of the answers you were looking for, but more than that, I hope you ended up with more questions than you started with. But that’s often what happens in the quest for knowledge, in the physical sciences, in mathematics, and now in AI research. Machine learning is currently a realm of paradoxes. ChatGPT can output very coherent and reasonable text for a wide variety of prompts, and then give bizarre results if you include inexplicable glitch words. GPT-4 can seem to reason about a complex situation, but then fail at basic logic. The complete structure of GPTs can be described in an essay, but their behavior defies analysis. “If we knew what we were doing, it would not be called research,” said Albert Einstein. Well, modern society is definitely doing research then, since we don’t know what we’re doing and we don’t know what our AIs are doing. I think we should keep that in mind, and try to find out.

Practical Details Unaddressed

I aimed to be as complete and detailed as possible, but there are several major practical details about GPTs and AI in general that I skipped over for the sake of brevity and clarity. For instance:

• A lot of the steps I described as splitting data into vectors and vectors into components are actually done in a single step by large matrix operations. The results are equivalent, but matrix operations are used because they are heavily optimized.
• Neural network training is not done using the gradient descent algorithm exactly as described here, but instead using a slightly modified version of the algorithm called stochastic gradient descent. Stochastic gradient descent only calculates the gradient at each step for a randomly selected subset of parameters, since this is far less computationally expensive.
• Although gradient descent is the basis of supervised learning, another article (or more) would be required to give a good overview of how training is done in practice. For instance, backpropogation, which is essential to making gradient descent practical, was only mentioned in this article.
• Some of the layers of GPT-3 (and presumably ChatGPT) use a modified version of attention called “sparse attention.” Sparse attention limits what nearby tokens a head can “look” at (beyond the limiting done already by the masking). Once again, this makes running the network faster and cheaper. (It can also have beneficial effects on how well the model works.)

Sources

My description of the inner workings of GPTs was based primarily on Jay Alammar’s articles The Illustrated Transformer and Illustrated GPT-2, and also Daniel Dugas’ article The GPT-3 Architecture, on a Napkin. To confirm that I had a correct understanding of certain points, I consulted Andrej Karpathy’s video Let’s build GPT: from scratch, in code, spelled out and also some of the original papers describing the techniques.