The Mandelbrot fractal is probably the most studied fractal and the most frequently implemented because of the simplicity of its calculation and the variety of the patterns found within it. Due to advances in CPU speed and browser JIT compilers, it is fairly trivial to create a renderer for the Mandelbrot set which uses double-precision floats in single-threaded Javascript and is still fast enough for comfortable interactive use. There are many renderers like this freely available on the internet. However, due to the precision limitations of 64-bit floating point numbers (also called “double precision floats” or “doubles”), at zoom levels where pixels represent a width less than about 10-16 on the complex plane, the images produced by these renderers become blocky and pixelated because the difference in the coordinates between adjacent pixels cannot be represented by a double-precision float. Both for the programming challenge and the sake of seeing more interesting images, various methods have been proposed to overcome this limitation and allow deeper zooms.
The most obvious solution is to use a software high-precision floating point or fixed point library, for instance based on Javascript BigInts. This method allows producing images at arbitrary depths, but at the cost of reducing performance significantly. Even one of the fastest Javascript arbitrary precision math libraries results in an over 500x slowdown compared to using native doubles for Mandelbrot rendering. (See https://github.com/charto/bigfloat#speed)
Clearly, some alternative which allowed high-precision zooming without the performance cost would be desirable. An investigation of algorithms used in desktop fractal programs provides a possible solution: perturbation theory. Essentially, a perturbation-based algorithm for rendering the Mandelbrot fractal leverages the fact that similarly located points tend to follow similar paths under iteration, at least at first. After first calculating the path taken by one point under iteration, the calculation of nearby points can be accelerated. Even more importantly, it is possible to only use high-precision math for this single “reference point”, and use native number types (32-bit single precision floats or 64-bit doubles) for the calculation of the neighboring points. The mathematical details of this method were first laid out by K. I. Martin in his short “Superfractalthing Maths” document.
Because the nearby points can be calculated accurately enough with only single precision floats, their calculation can be done on the GPU in WebGL. (WebGL only supports single precision floats.) This very significantly speeds up rendering time because GPU is highly parallelized. Thus a composite rendering architecture is suggested: the slow calculation of a reference point is done single-threaded on the CPU in Javascript using a software arbitrary precision library, and the comparatively quick calculation of nearby points based on the results of this reference is done on the GPU in WebGL using native WebGL single-precision floats.
There are at least two online renderers which implement this rendering architecture: “deep-mandelbrot” by munrocket, and “facts” by charto/jjrv. I found both renderers somewhat lacking in features and wanted to gain the experience of implementing this rendering architecture. This Advanced Studies project is the result of that desire.
The program I eventually implemented is not an easily usable renderer like the two programs mentioned above. Rather, it should be seen as a proof of concept of the architecture useful for further experimentation. The code I wrote for this project consists of four main components: a simple utility library to simplify interaction with the WebGL API, a Javascript function to perform the reference point calculation with arbitrary precision math, a WebGL shader to perform the nearby point calculation with single precision math, and a HTML5 UI to view the results of the calculations and modify parameters interactively. There are also a few other minor components. For arbitrary precision math, the program uses the “bigfloat” package. My own reactive DOM library (Dynein) powers the HTML5 UI and handles triggering a rerender when parameters change. I wrote all of my Javascript code in Typescript for better editor support and compile-time error checking.
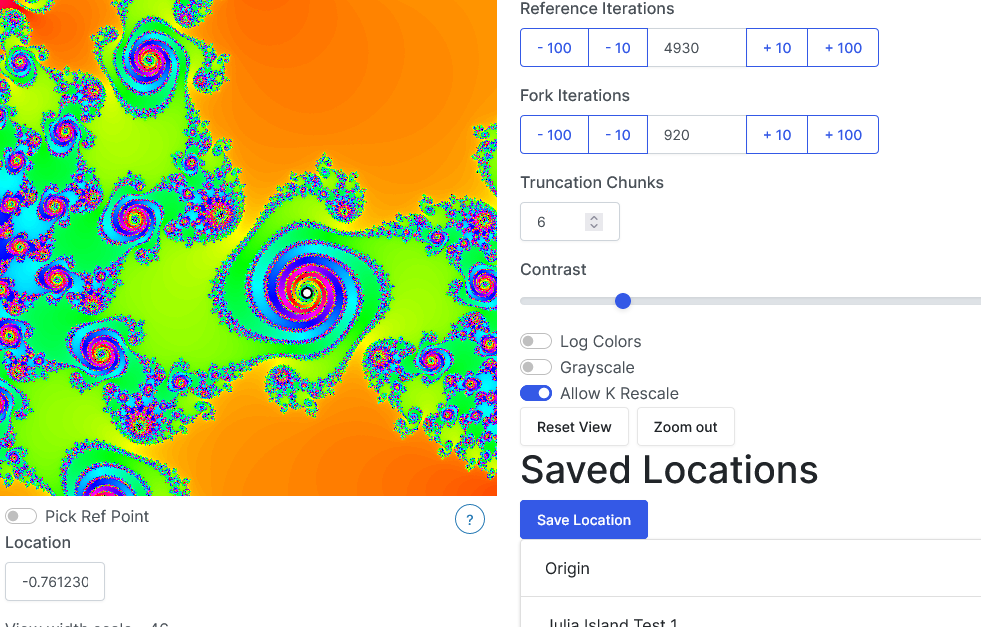
A screenshot of the program in operation is shown below:

The upper left quarter of the screen shows the render output. Clicking on the image zooms in and sets a new view center position, or sets the reference point location (represented by a white dot). The lower left quarter contains an input box for the view position and zoom level, along with view of various values and coefficients from the CPU calculation. The first three inputs in the upper right corner (Reference Iterations, Fork Iterations, Truncation Chunks), control, respectively, the max iterations on the CPU, the max iterations on the GPU, and the precision of the CPU calculation. The next three inputs and toggle switches on the right side of the screen control various aspects of the coloring formula. The “Allow K rescale” toggle controls a slight modification I made to the algorithm which seemed necessary for the practical implementation of deep zooming and is explained in more detail in the code. The “Saved Locations” area allows users to persistently save and load the algorithm parameters for a location of interest. Several locations are pre-loaded into the program.
The algorithm was implemented successfully (the screenshot above shows a render at a pixel size around 10-238, far below the 10-16 possible with Javascript doubles) although more testing perhaps with a desktop program would be necessary to confirm the correctness of the results. But even if the algorithm is correct, more development would be necessary to make a fully useable renderer. For reasons which I do not fully understand, it does not seem to be possible to zoom in near “mini-Mandelbrots” using this program. When attempting it, it does not seem to be possible to pick any combination of parameters and reference point location which gives a correct image.
There are several paths for further development of this program. The most important feature to be added would be fixing the problem mentioned above to allow exploring near mini-Mandelbrots, which are usually the most interesting locations in the fractal. The source code for other renderers implementing the perturbation algorithm could be inspected to better understand the proper solution. Other algorithm improvements could include automatic reference point selection, multiple reference points per image, and automatic rendering glitch detection and correction using the algorithm used in desktop software. The UI might also be improved to allow multiple color palettes, full-screen view, and easy image export.
Despite its limitations, the program does allow far deeper zooms than possible using native doubles and is far more performant than using arbitrary precision math for every pixel (its also faster than using CPU double precision math for every pixel). It thus fulfilled the project requirements and the implementation process gave me a hands-on understanding of the difficulties of implementing the Mandelbrot perturbation algorithm. I think it will be a good starting point for a full-featured in-browser deep-zooming program.